After a difficult start, space launchers now take off from Florida with metronome regularity, and their reusable first stage returns to land smoothly and completely autonomously on barges installed at sea. This undeniable American technological success has of course given ideas to all the space powers on the planet, and Europe is not to be outdone.
The object of Etienne Bertin's thesis is in line with this. The smooth return to Earth of a first stage implies the respect of very strict safety constraints. It is necessary to determine a trajectory which allows to reach the landing zone with a zero velocity and a perfect verticality, without which it is the assured crash. It turns out that the planning of this trajectory can be done by solving an optimal control problem, a discipline particularly mastered at ENSTA Paris, whether in the Applied Mathematics Unit (UMA) or in the Computer Science and Systems Engineering Unit (U2IS).
Several trajectories allow this safe return of the launcher. But only one allows to maximize at the same time a crucial parameter in the context of commercial flights, the one that minimizes fuel costs.
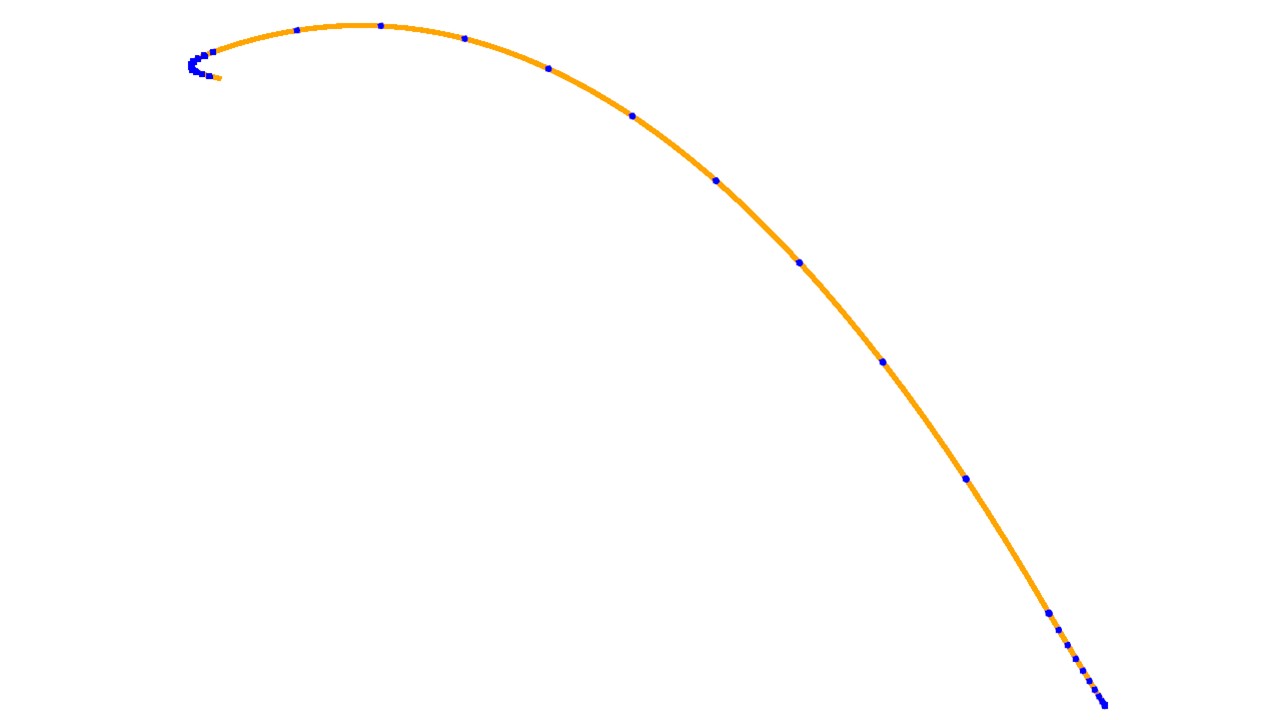
Typically, the mission profile is as follows: after tearing off the entire launcher from the launch pad, the first stage detaches from the upper stage and lets it continue on its way to launch the payload. It cuts its engines to let itself fall, then reactivates them to return towards its starting point before continuing its trajectory in a ballistic way.
At the end of thrust, it turns over to put its engines again in direction of the Earth. Halfway, it reignites the engines to brake and not to risk the explosion of the tanks because of a heating consecutive to the friction with the atmosphere. Finally, a last ignition, more powerful, allows to dissipate the energy accumulated during the fall and to land gently.
In reality, this ideal trajectory is rarely followed. The first reason is that one of the crucial parameters, the maximum thrust of the rocket engines, is rarely nominal and constant, and can vary in significant proportions. The second reason, which is a corollary of the first one, is that one is never really sure of the exact place where the return trajectory will start. You can therefore miss the recovery zone. In the end, mission planners are confronted with a whole continuum of uncertainties, leading to a set of scenarios in which the rocket does not return safely.
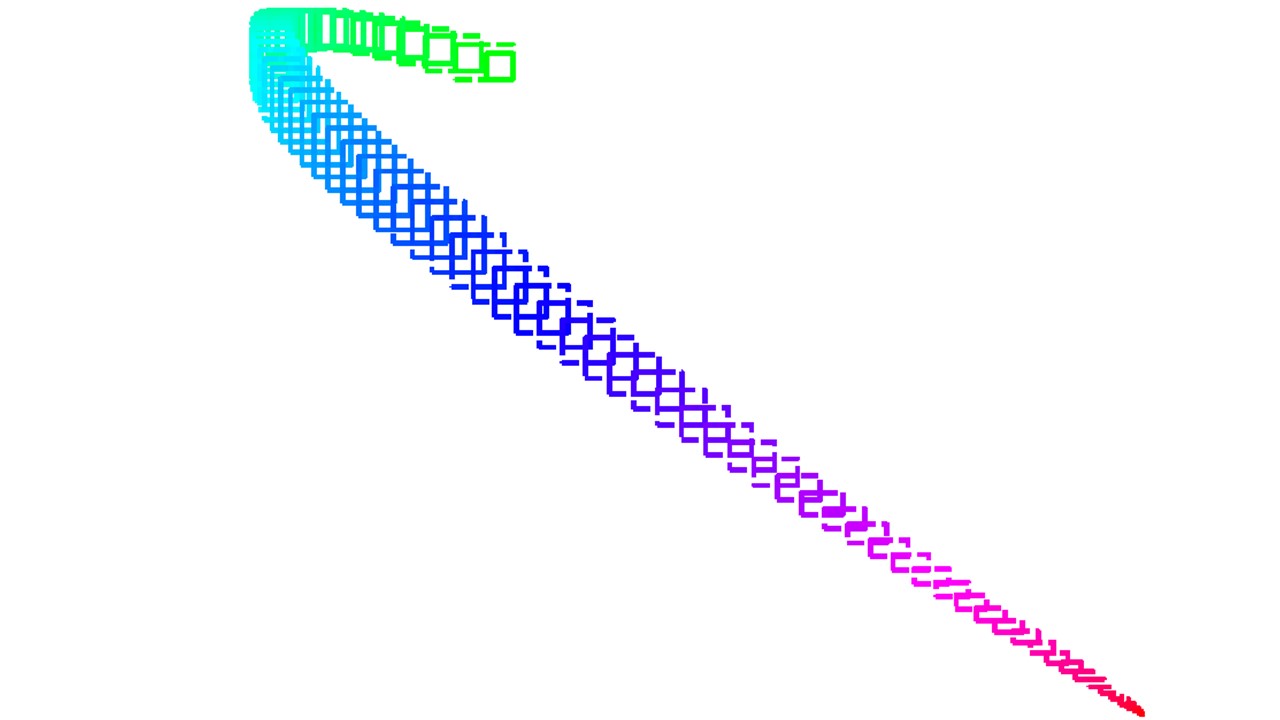
The solution studied by Etienne Bertin consists in placing bounds on these fatal uncertainties, so that we can guarantee the safe return of the first stage. It is a matter of calculating a virtual "tube" that guarantees to frame all possible solutions of this optimal control problem.
To do this, two tools must be used: assembly methods, which allow us to frame all the possible trajectories of a model with uncertainty whose dynamics are known, and optimal control, which allows us to calculate the desired control and the trajectory that goes with precision.
By deploying these methods, Etienne Bertin demonstrated in his thesis that it was possible to define sets of optimal trajectories in problems with bounded uncertainties by proposing trajectory framing methods using zonotopes, symmetric polygons whose machine representation offers many computational tricks. He used this result to develop a program to frame sets of optimal trajectories, and to evaluate their performance.
Future work will increase the amount of tolerable uncertainty in the problem by improving its geometry.
This work has been published in the international journal Acta Cybernetica, presented at the international conference CDC 2021, and communicated in seminars and workshops: SWIM2019, Journées SAGIP, International Online Seminar on Interval Methods in Control Engineering.