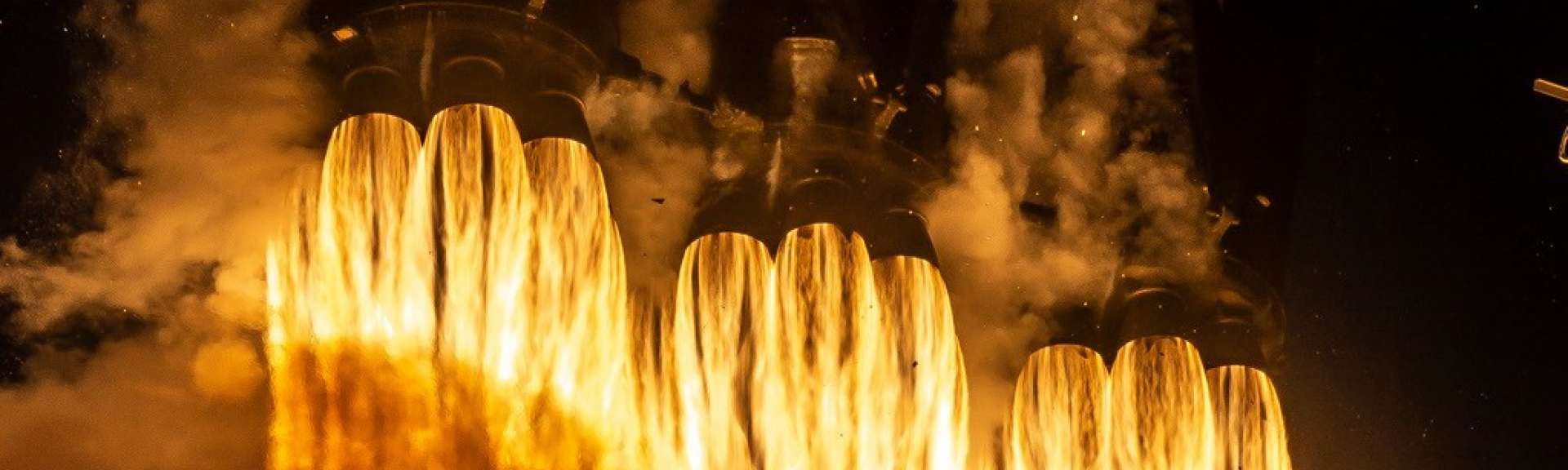To the credit of all the traditional space agencies that had given up on finding a solution, it has to be said that this first-stage return is fraught with pitfalls, which engineers call hazards. There are essentially three of them: fluctuating propulsive flow, the exact amount of fuel remaining, which has a direct influence on flight dynamics, and the system's overall aerodynamics, which vary with altitude.
In her thesis "Optimal control under uncertainties for the vertical landing of a reusable launcher's 1st stage", defended last September at ENSTA Paris, Clara Leparoux, supervised by Frédéric Jean, director of the Applied Mathematics Unit at ENSTA Paris, and Bruno Hérissé of ONERA, developed an optimal control technique that takes these uncertainties into account.
One of the supervisors, Frédéric Jean, has long been working on planning with optimal control. In this case, the aim was to find the best trajectory for a given criterion, while taking account of hazards, which meant adding robustness to planning.
A decisive criterion in the case of a space launcher is the minimization of fuel consumption. Anything that can be saved up to the final phase ensures that the braking thrust will be sufficiently powerful and prolonged to guarantee a smooth landing.
The usual strategy in planning with optimal control is to plan for optimality first, then use in-flight measurements to recalibrate and correct errors as the flight progresses.
Clara Leparoux's thesis work highlighted the fact that this approach has a limit: the optimal trajectory obtained theoretically may be impossible to achieve in the end, due to hazards.
It is therefore advisable to use a planning method based on stochastic modeling (produced by the effect of chance) rather than deterministic modeling. We then add "noise" to model the lack of knowledge of the initial conditions, interpreting it as a random variable. Launcher dynamics are modeled in the same way.
Robustness will be modeled by setting as a criterion the minimization of both fuel consumption and trajectory dispersion around the mean.
In her thesis, Clara Leparoux proposes a good approximation method for dealing with this type of problem, replacing it with a much simpler deterministic problem to which standard algorithms can be applied to minimize computation time.
This method allows us to take into account probability constraints, such as guaranteeing that the launcher will hit the target with a probability greater than 95%.
In the end, this thesis work has provided a general framework with a satisfactory numerical resolution method thanks to a suitable approximation.