In the case of so-called "slender" structures, such as pipes or cables, which may be partially buried in a fluid medium (as is typical of nuclear power plants), these structures act as waveguides that can propagate acoustic waves over long distances.
However, non-destructive testing of buried guides presents two major difficulties: firstly, only one side of the structure to be tested can be accessed, the other being buried or submerged, and secondly, the waves used to probe the structure tend to leak partially into the medium surrounding the buried part.
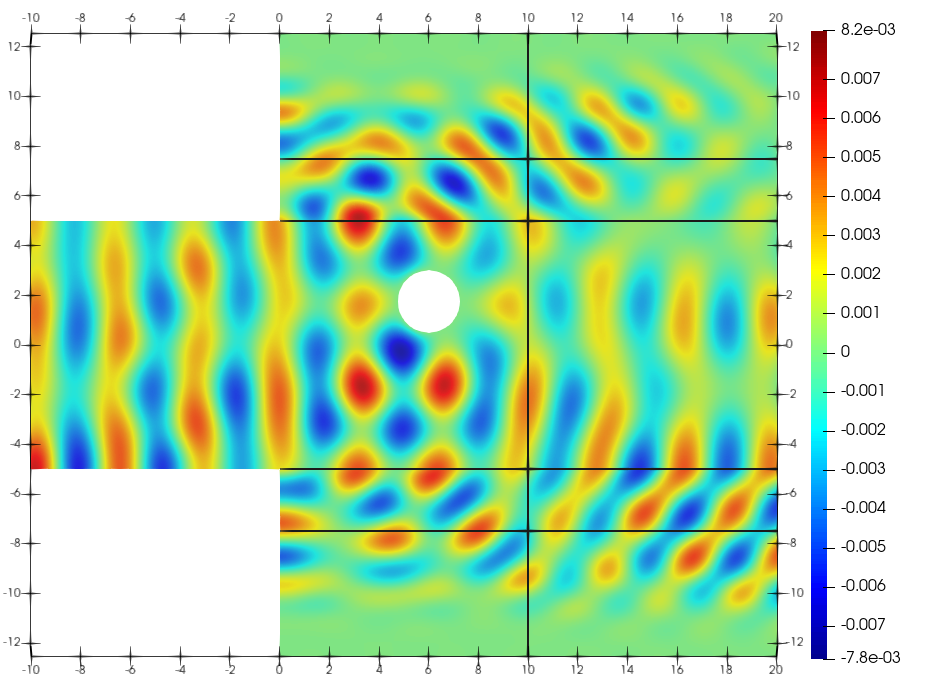
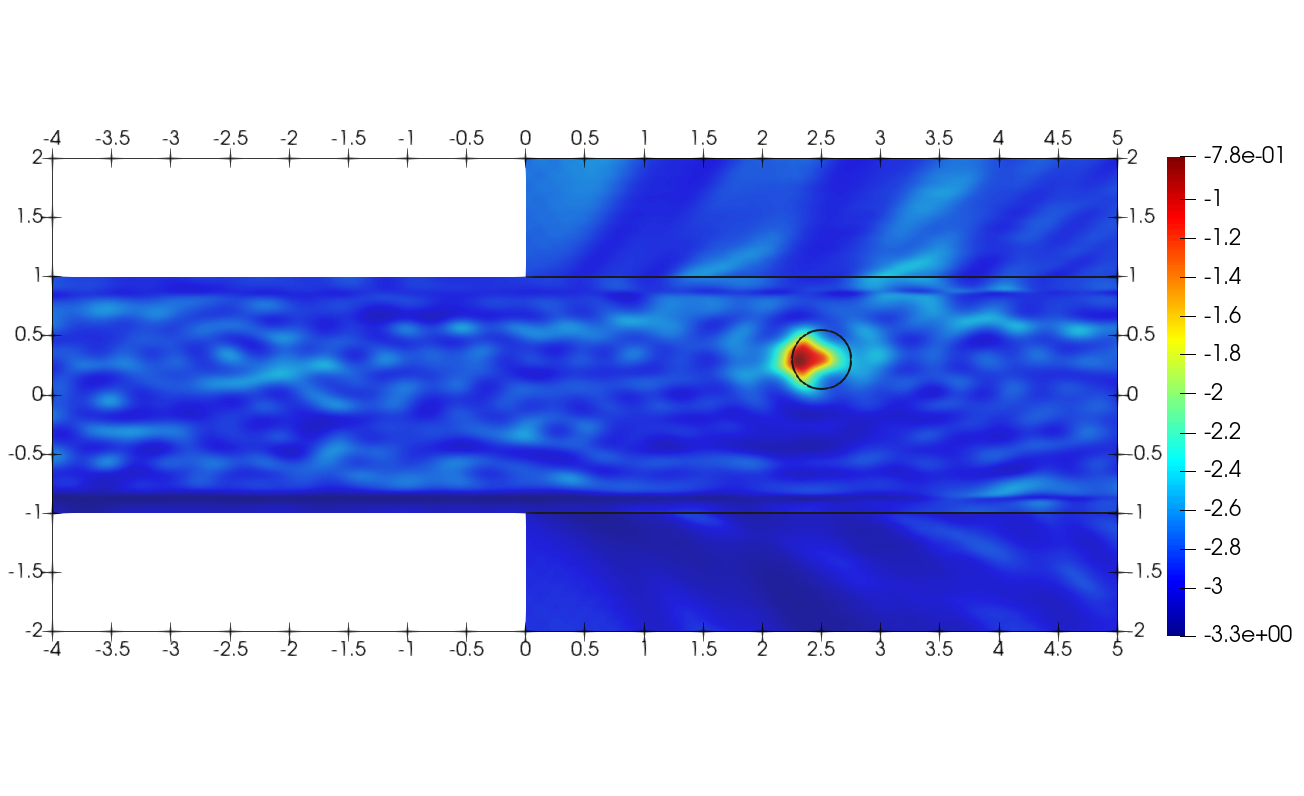
The aim of Jean-François Fritsch's thesis was to assess the feasibility of using a Linear Sampling Method in this particular case, which involves gridding the area to be inspected and determining for each grid point whether or not it lies within a defect, using a mathematical criterion based on measurements.
Several steps were necessary to achieve this. First, we had to work on a simplified version of the problem, considering a structure behaving like a fluid from the point of view of waves. The equations, well mastered in this case, made it possible to justify the method and move on to the next stage: the study of an elastic structure partially immersed in a fluid, which corresponds to a more complex vector problem.
In his thesis, Jean-François Fritsch addressed both the direct problem of wave propagation and associated diffraction phenomena, and the inverse problem of imaging. He succeeded in demonstrating that the LSM sampling method can indeed detect defects in a partially immersed slender structure, even if the accuracy is less good than in the case where the structure is not immersed.
This thesis has already given rise to 3 scientific publications and a patent application.
This work was directed at ENSTA Paris by Laurent Bourgeois and Christophe Hazard, and supervised by Vahan Baronian and Arnaud Recoquillay for CEA, and with the collaboration of Sonia Fliss (ENSTA Paris).