Ce qui frappe d’emblée lorsqu’on s’entretient avec Nastassia Pouradier Duteil, c’est sa profonde et franche modestie. Ainsi, quand on lui demande pourquoi elle a choisi de faire une prépa scientifique plutôt que littéraire alors qu’elle était également passionnée par les deux domaines, la chercheuse donne une réponse pour le moins surprenante : « Je n’ai pas une très bonne mémoire. Or les mathématiques demandent peu de mémoire, mais surtout de la logique. Quand on a compris les concepts, la logique, tout peut se redémontrer. C’est très rassurant pour quelqu’un comme moi qui ai du mal à retenir. »
Et lorsqu’on lui fait remarquer que, pour quelqu’un qui n’a pas une très bonne mémoire, elle pratique tout de même 5 langues couramment, dont le russe, elle a là encore une explication qui ne met guère en avant ses propres mérites :
« De 10 à 13 ans, j’étais dans une école internationale en Thaïlande où les cours étaient en anglais, j’ai donc été placée très vite en immersion dans cette langue. Le russe, c’était un choix de ma part car j’ai des origines russes, mais trop lointaines pour que cette langue soit encore parlée dans ma famille. Je l’ai donc apprise par correspondance. Et c’est d’ailleurs à ENSTA Paris que j’ai eu pour la première fois un prof de russe en chair et en os devant moi ! »
Nastassia Pouradier Duteil revient en France en classe de 3e, avec une conviction chevillée au corps : « Je me souviens m’être dit à mon retour que je repartirais à l’étranger dès que j’en aurai l’occasion, et m’étais fait la promesse intérieure de faire au moins la moitié de mes études à l’étranger. J’ai réussi à la tenir, en partie grâce à mes études à ENSTA Paris et sa grande ouverture à l’international. »
Avant cela, il lui faut déjà obtenir son baccalauréat au terme de ses études secondaires qu’elle effectue à la Cité Scolaire Internationale de Lyon.
« Même si j’ai choisi une filière scientifique, du fait du caractère international de ce lycée, j’ai eu jusqu’au bac des heures de plein d’autres matières, en particulier de la littérature et de l’histoire-géographie. J’ai adoré avoir cette formation très complète jusqu’à la fin de la terminale ! »
Puis elle enchaine avec une prépa scientifique aux Lazaristes de Lyon.
« Quand j’ai entendu parler du concept de la prépa, cela m’a très bien convenu car cela laissait beaucoup de portes ouvertes. Même si j’ai trouvé ces deux années très dures, c’était une bonne manière de prolonger de façon intensive l’étude des matières scientifiques que j’aimais le plus. Mais à cette époque je ne savais pas du tout quel métier je voulais faire, même si le concept et le rêve de chercheuse me trottait un peu dans la tête, mais sans avoir aucune idée de ce en quoi ça consistait. »
Quand vient l’heure des concours et des choix, l’option ENSTA Paris se profile très vite.
« Je m’étais renseignée et avais entendu dire qu’ENSTA Paris était une école très scientifique, par rapport à d’autres écoles, où peut-être on formait plus rapidement les étudiants à des matières managériales. A l’inverse, ENSTA Paris avait une première année encore très ouverte sur de nombreuses disciplines scientifiques, et aussi un vaste choix de langues et de cours de culture générale. J’avais encore besoin de ce temps pour me déterminer. Je voulais, là encore, garder le plus de portes ouvertes le plus longtemps possible. »
Nastassia garde un très bon souvenir de ses années à ENSTA Paris :
« Ça m’a donné une vaste culture scientifique qui m’est encore utile aujourd’hui. J’ai apprécié d’avoir cette ouverture sur un large éventail de sciences. Sur le plan des matières scientifiques, le cours que j’ai le plus aimé a été celui de géométrie différentielle de Frédéric Jean : c’est là que j’ai découvert le concept de variété différentielle, qui m’a marquée dès ce moment-là et qui m’a servi pendant ma thèse. J’ai aussi beaucoup apprécié les cours de mécanique des fluides de Sabine Ortiz, qui nous a enseigné des notions dont je me souviens encore. Et aussi tous ces cours de culture, sur des sujets totalement inattendus, comme l’ethnologie, l’histoire de l’art ou l’Opéra. J’ai conservé de très belles amitiés parmi mes camarades de promotion. C’est une école à taille humaine, avec une vie étudiante très chaleureuse, on se connaissait tous et toutes. »
En attendant de répondre à l’appel du grand large, c’est avec le monde de la recherche que Nastassia fait connaissance au cours de son stage de recherche de 2e année, une autre particularité du cycle ingénieur d’ENSTA Paris.
« A cette époque, j’adorais les mathématiques mais je me demandais aussi à quoi ça allait bien pouvoir me servir. J’ai donc essayé de trouver un stage qui réponde au moins en partie à la question. Un Professeur du laboratoire Jacques-Louis Lions, Yvon Maday, proposait un sujet de stage en collaboration avec Ubisoft, le célèbre éditeur de jeux vidéo. L’idée était de répondre avec des outils mathématiques à la question de la simulation de l’éclairage dans les jeux, comment le rendre le plus naturel et réaliste possible. J’avais trouvé que c’était une jolie application des mathématiques. »
Autre particularité du cycle ingénieur d’ENSTA Paris, sa grande ouverture sur l’international notamment par le jeu de ses accords de double diplôme.
« C’était tout ce dont je rêvais ! J’étais donc ravie que ce soit vu comme un point positif dans notre scolarité ! »
Pour Nastassia, cette ouverture à l’international prendra principalement la forme d’une année de césure à l’Université Technique d’État de Moscou.
« Du fait de mes origines familiales, j’avais une vision un peu fantasmée de la Russie depuis mon enfance. Et de fait, c’est un pays très contrasté, avec du très beau, mais aussi du très triste, encore plus aujourd’hui… mais j’ai fait des rencontres extraordinaires là-bas, et j’y ai gardé de solides amitiés. Ça m’a aussi apporté une autre façon de voir les mathématiques. »
De retour en 3e année à ENSTA Paris en 2012, Nastassia Pouradier Duteil choisit de faire un double master en parallèle de celui de modélisation de l’École. Familiarisée avec le laboratoire Jacques-Louis Lions lors de son stage de recherche de 2e année, elle opte pour celui proposé par ses professeurs qui s’appelait à l’époque « Analyse numérique et équations aux dérivées partielles ».
« Assez logiquement, c’est cette 3e année qui m’a permis de trouver ma voie sous la forme d’un sujet de thèse. Emmanuel Trélat, aujourd’hui directeur du laboratoire Jacques-Louis Lions, donnait un cours de contrôle des équations différentielles. Ce que j’aimais bien dans ce cours, c’était le fait qu’on utilise des outils mathématiques pour répondre à des questions pratiques : comment contrôler un système pour atteindre un état donné, des questions qui m’intéressaient beaucoup. J’en étais à 5 ans en France, et comme je m’étais promis de faire une partie de mes études à l’étranger, je ne rêvais que de repartir. Cet ailleurs, ça a été cette fois les États-Unis, à Rutgers, l’université d’État du New Jersey, pour faire de la théorie du contrôle appliquée à la biologie. »
Cette première confrontation à la biologie est pour Nastassia Pouradier Duteil une véritable révélation.
« Cela m’a obligée à quitter le domaine de la pureté mathématique pour aller voir concrètement dans les labos comment ça se passe. Modéliser le vivant est passionnant mais demande de faire encore plus de concessions que lorsqu’on modélise la physique. Tout ce qu’on peut faire avec les mathématiques, c’est choisir quels aspects du système qu’on est en train d’étudier on veut prendre en compte dans le modèle, sachant qu’on va être obligés de laisser tomber tout un pan du système. Le choix des variables à retenir se fait en discutant avec les biologistes, et cet aspect a été une partie de ma thèse que j’ai beaucoup appréciée ».
Un intérêt qui ne s’est pas démenti puisque un an après sa soutenance de thèse en 2017, Nastassia Pouradier Duteil est devenue chargée de recherche dans l’équipe-projet MAMBA (devenue MUSCLEES) commune à Inria, Sorbonne Université et le CNRS, qui applique la modélisation à la biologie et à la médecine.
« Au cours de ma thèse, j’ai appris grâce à mon directeur, Benedetto Piccoli, à communiquer avec les biologistes, qui forment une communauté scientifique très différente de celle des mathématiciens et mathématiciennes. Benedetto arrivait à présenter le modèle mathématique et à poser les questions de façon à ce que les biologistes puissent participer à l’élaboration du modèle, que ce ne soit pas juste un résultat livré par les mathématiciens, mais quelque chose de construit ensemble. C’est un aspect de mon travail que je trouve passionnant. »
Et pas forcément le plus simple.
« Là où nous avons le plus de points de désaccord entre les deux communautés, c’est qu’en mathématiques, on essaie de simplifier, alors que les biologistes veulent prendre en compte le plus de phénomènes possibles. Quand quelque chose ne marche pas, les biologistes sont tentés de rajouter des paramètres qui manqueraient au modèle, là où les mathématiciens et mathématiciennes voudraient plutôt enlever tout le superflu pour se retrouver avec la colonne vertébrale du problème et voir si ça ne suffirait pas. »
Au premier abord, on pourrait croire que les mathématiques se mettent gracieusement au service de la biologie, sans que la discipline n’en tire aucun bénéfice pour elle-même. Mais bien souvent, d’étonnantes boucles de rétroaction se mettent en place qui permettent aux deux disciplines de développer une véritable symbiose.
« Il y a eu un tel essor des collaborations entre mathématiques et biologie ces 30 dernières années que les mathématiciens se régalent de toutes les opportunités qu’apporte la biologie pour étudier de nouveaux modèles, avec des exemples magnifiques de modèles mathématiques qui viennent au départ d’un phénomène biologique » s’enthousiasme la chercheuse.
Ainsi en est-il du modèle de Keller-Segel, au départ utilisé en biologie pour décrire le phénomène de chimiotaxie, c'est-à-dire le mouvement orienté de micro-organismes, comme les bactéries, en réponse à des gradients de concentration chimique (souvent une substance qui les attire, comme des nutriments).
Le modèle comprend deux équations principales, une pour la densité de population des bactéries, et l’autre pour la concentration chimique, décrivant par exemple sa diffusion, ou son taux de production ou de consommation par les micro-organismes. Ces deux équations sont couplées, ce qui signifie que la densité de la population influence la concentration chimique, et vice versa. Par exemple, les bactéries se déplacent vers des régions avec une forte concentration de nutriments, mais en même temps, elles consomment ces nutriments, modifiant ainsi le gradient chimique.
« Il y a énormément de travaux en mathématiques pour savoir quels sont les paramètres qui permettent une concentration de la population » reprend la chercheuse.
« Mathématiquement, il peut y avoir explosion de la population en un point en temps fini. Ça n’a rien à voir avec ce qui se passe en biologie (toutes les bactéries ne peuvent pas s’agglutiner en un même point exact de l’espace, c’est physiquement impossible), mais mathématiquement on sait qu’il y a des paramètres du modèle qui produisent cet effet. Et ça amuse beaucoup les mathématiciens de tenter de déterminer quels sont ces paramètres ! Par exemple, dans la version simplifiée du modèle, il y a un paramètre fondamental : la masse initiale de la population de bactéries. Il a été prouvé que lorsque ce paramètre est au-dessus d’une valeur seuil de 8 pi, il y a cette explosion en temps fini, et en dessous de cette valeur, elle n’a pas lieu. L’étude théorique mathématique de différentes versions de ce modèle est allée très loin et continue aujourd’hui sans qu’il n’ait forcément un rapport avec la biologie ! En revanche, il est très important de comprendre les différents comportements qui peuvent être engendrés par le modèle, et certains de ces comportements nous permettent d’aider à expliquer les phénomènes biologiques. »
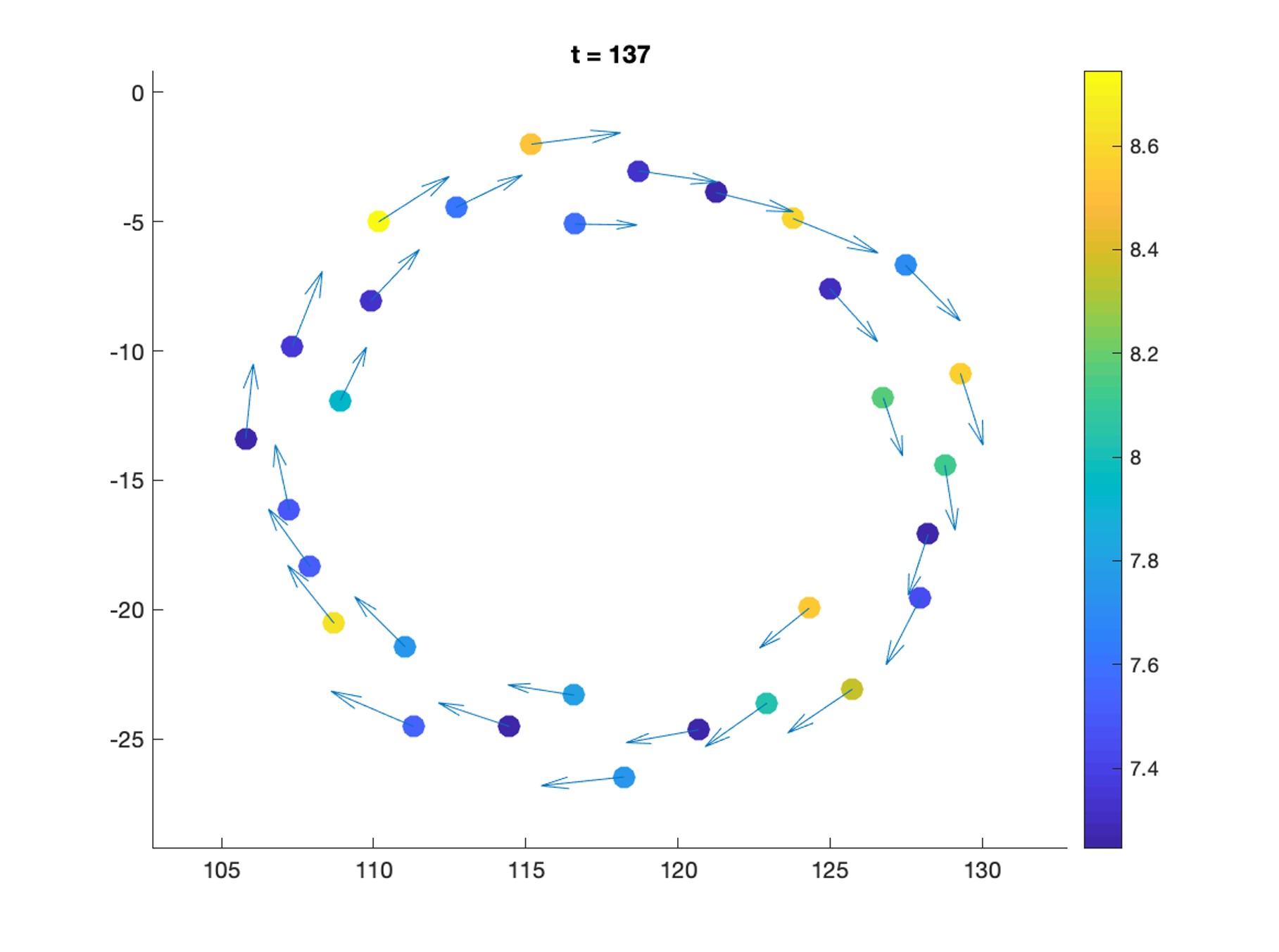
Au quotidien, Nastassia Pouradier Duteil étudie la modélisation mathématique de tout ce qui est en lien avec les dynamiques collectives, c’est-à-dire les dynamiques qui régissent les populations, quelles qu’elles soient : bactéries, oiseaux, poissons, humains. Cela veut-il dire que les êtres humains, en foule, sont régis par les mêmes lois que les bactéries ?
« Oui et non » répond la chercheuse. « Si on va dans les détails de ce qu’on est en train de modéliser, il y a des caractéristiques qui différencient tous ces problèmes ; mais quand on fait le travail d’abstraction des mathématiques pour arriver à une équation très simple, on arrive souvent à une même équation qui régit en effet toutes ces populations, aussi différentes soient-elles à priori. »
La grande question qui anime les chercheurs et chercheuses qui travaillent sur ce sujet est la suivante : comment les grands groupes arrivent-ils à s’organiser sans qu’il y ait de contrôle ou de chef ?
« On considère généralement que les individus ont des interactions locales les uns avec les autres, avec leurs plus proches voisins, ou avec les gens qui sont dans leur cercle d’amis si on prend le cas des humains. Il y a des structures à la fois spatiales et familiales qui jouent. Mais la partie importante est que la communication entre les individus est locale, et n’a lieu qu’entre un individu et quelques autres, très peu nombreux. Pourtant, lorsqu’on regarde le groupe dans son ensemble, il y a une organisation globale qui apparaît. Et là on peut penser à plein de phénomènes naturels : cellules qui se concentrent à un même endroit, mais aussi auto-organisation des foules. »

Les couloirs du métro parisien, souvent bondés aux heures de pointe, offrent un bon exemple de cette auto-organisation : si deux flux de personnes vont l’un contre l’autre, il va y avoir une tendance spontanée à former une file dans chaque sens, de façon à fluidifier la circulation, sans pourtant que personne ne prononce un mot ou n’indique de consigne.
« On observe la même chose avec les poissons qui se mettent à tourner autour d’un centre commun, ce qu’on interprète au départ comme un mouvement réflexe de protection contre les prédateurs, et qui se propage par imitation. Il y a aussi l’exemple des nuées d’oiseaux qui évoluent à grande vitesse, où les volatiles parviennent la plupart du temps à s’éviter alors qu’ils peuvent être des dizaines de milliers d’individus dans les vols d’étourneaux, tout ça de façon synchronisée... Comment arrive-t-on à cette auto-organisation globale à partir d’interactions locales ? Même si beaucoup de réponses ont déjà été apportées, cela reste un sujet de recherche. Et comme on retrouve ces modèles dans beaucoup de domaines, il y a toujours des questions ouvertes sur ces sujets. »

Mais après nous avoir amenés à l’exercice d’humilité un peu douloureux consistant à nous considérer, pris dans une foule, comme n’ayant guère plus de libre arbitre qu’une bactérie, Nastassia nuance le propos et nous laisse espérer un sort meilleur :
« Ce qui m’intéresse actuellement, c’est de commencer à différencier les individus les uns des autres. La plupart des recherches faites jusqu’à maintenant considèrent que tous les individus sont des copies parfaites les uns des autres, alors qu’en fait ils ont nécessairement des caractéristiques différentes, ce ne sont pas des clones. Ces différences entre les individus peuvent jouer sur le comportement global. Et ça a un impact direct sur la façon de modéliser les foules. »
Avec encore de très nombreux intérêts de recherche sur le sujet, Nastassia Pouradier Duteil n’en a pas fini d’étudier les foules et leurs caractéristiques, mais aussi les étonnantes propriétés mathématiques qu’elles peuvent contribuer à faire émerger. Quelle voie prendra la suite de sa carrière de chercheuse ? Manifestement, aucun modèle ne saurait prédire les chemins de sa créativité. Et c’est plutôt une bonne nouvelle, laissant augurer favorablement de tout ce qu’elle peut encore contribuer à découvrir sur le comportement des foules.